In this task students investigate and ultimately prove the validity of the method of generating Pythagorean Triples that involves the polynomial identity (x 2 y 2) 2 =(x 2y 2) 2 (2xy) 2 Type ProblemSolving Task I am trying to solve the equation $$ (x^2y^2)y' 2xy = 0 $$ I have rearranged to get $$ y' = f(x,y) $$ where $$ f(x,y) = \frac{2xy}{x^2y^2} $$ From here I tried to use a trick that I learned Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow,Add − x 2 y 2 x 2 y 2 and x 2 y 2 x 2 y 2 Add x 2 x 2 x 2 x 2 and 0 0 Simplify each term Tap for more steps Multiply x 2 x 2 by x 2 x 2 by adding the exponents Tap for more steps Use the power rule a m a n = a m n a m a n = a m n to combine exponents Add 2 2 and 2 2
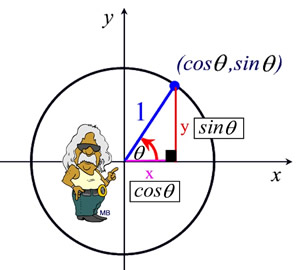
Pythagorean Identities Mathbitsnotebook Ccss Math
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples-Write a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) areFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the square of a binomial, etc




Understanding Pythagorean Identities Studypug
For x^2y^2=2xy, we get (by differentiating implicitly), dy/dx =1 That's the same as the derivative of a linear function with slope, 1 Hmmmmm Let's see If we have x^2y^2=2xy The we must also have x^22xy y^2=0 Factoring gets us (xy)^2 = 0 And the only way for that to happen is to have xy=0 So y=x and dy/dx =1X2 y2 can be written as (xy)2 this is in the form of (a b)2 = a2 2ab b2 so the above can be written as x2 2xy y2 or there is another one too x2 y2 = (xy) (x yX^ {2}2yxy^ {2}=0 x 2 2 y x y 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2y for b, and y^ {2} for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0
The reference for Conic Section General Cartesian form tells you how to determine what conic section it is, when given the General Cartesian form #Ax^2 Bxy Cy^2 Dx Ey F = 0# Here is the given equation in the general form #2x^2 4y^2 8 = 0# Please observe the value of #B^2 4AC = 0^2 4(2)(4) = 32#The reference says that this is an ellipseIdentity (x 2 y 2)2 = (x 2 – y2)2 (2xy) 2 can be used to generate Pythagorean triples NCN8 () Extend polynomial identities to the complex numbers For example, rewrite x 2 4 as (x 2i)(x – 2i) NCN9 () Know the Fundamental Theorem of Algebra;For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples CCSSMathContentHSAAPRC5 () Know and apply the Binomial Theorem for the expansion of ( x y ) n in powers of x and y for a positive integer n , where x and y are any numbers, with coefficients determined for example
The polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples D Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms;Generate Pythagorean Triples using an identity About this video In this lesson you will learn to generate a Pythagorean Triple by using the identity (x^2 y^2)^2 (2xy)^2 = (x^2 y^2)^2MGSE912AAPR4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples Video Lessons ( p1, p2a,



Pythagorean Triples




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Interpret functions that arise in applications in terms of the context MGSE912FIF4 Using tables, graphs, and verbal descriptions, interpret the key characteristics of a function which models the relationship4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples With the increase in technology and this huge new thing called the Internet, identity theft has become a worldwide problemWrite a(x)/b(x) in the form q(x) r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the



2




The Pythagorean Theorem Educational Outreach
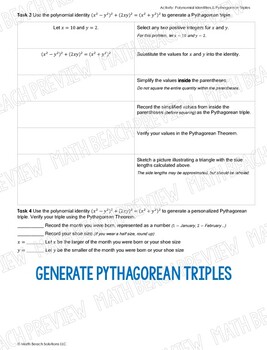
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Use complex numbers in polynomial identities and equations MGSE912NCN8 Extend polynomial identities to include factoring with complex numbersExample, the polynomial identity (x2 y2) 2 = (x2 – y 2) 2 (2xy)2 can be used to generate Pythagorean triples 8) AAPR6 Rewrite simple rational expressions in different forms;Students will prove the polynomial identity ( x^2 y^2 )^2 ( 2xy )^2 = ( x^2 y^2 )^2 and use it to generate Pythagorean triplesUse this activity as independent/partner practice or implement it as guided notes and practice for students in need of extra supportThis activity is in PDF formatPar
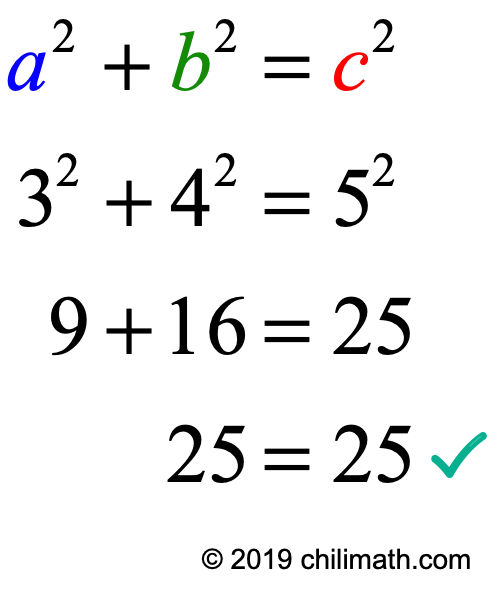



Generating Pythagorean Triples Chilimath



Arxiv Org Pdf 1902
CCSSMathContentHSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Authors National Governors Association Center for Best Practices, Council of Chief State School OfficersTap for more steps Add 1 1 to both sides of the equation x 2 y 2 2 x 2 y = 1 x 2 − y 2 − 2 x − 2 y = 1 Complete the square for x 2 2 x x 2 − 2 x Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = 2, c = 0 a = 1, b = − 2, c = 0Identity (x2 y2)2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Desired Student Performance A student should know • Number theory • Consecutive numbers forms A student should understand



2



2
2 Using suitable identities find (1092)2 3 Using the identity (ab)2 = a2 2ab b2, find (5a 7b)2 4 Find 194 * 6 using suitable identity 5 Use a suitable identity to find the product of (3a 1/3)(3a 1/3) 6 The length and breadth of a rectangle are 3x2 2 and 2x 5 respectively Find its areaGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Tangent of x^22xyy^2x=2, (1,2) \square!



Www Jstor Org Stable 10 4169 College Math J 48 2 115




6 The Abc S Of Number Theory
For example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples I can prove polynomial identitiesNumerical relationships For example, the polynomial identity (x2 y2)2 = (x2 – y 2) (2xy) can be used to generate Pythagorean triples AAPR5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example byFinding x and yintercepts given a polynomial function Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples TD



Www Jstor Org Stable



Www Clarenceschools Org Cms Lib Ny Centricity Domain 465 Notes proving identities Pdf
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Rewrite rational expressions AAPRD6Establish the identity (1 sin^2(x))(1 tan^2(x)) = 1Identity (x2y2)2 = (x2– y2)2 (2xy)2 can be used to generate Pythagorean triples Eureka Math 1 Lesson 2 –7 Module 1 Lesson 10 MP1 Make sense of problems and persevere in solving them Students discover the value of equating factored terms of a polynomial to zero as a means of solving equations involving polynomials Eureka Math




Pythagorean Identities Mathbitsnotebook Ccss Math



Algebra 2 Math Test Item Specifications Final May 16 Flip Ebook Pages 1 50 Anyflip Anyflip
For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples ASSE Use the structure of an expression to identify ways to rewrite it For example, see x 4 y 4 as (x 2) 2 (y 2) 2, thus recognizing it as a difference of squares that can be factored as (x 2 y 2)(x 2 y 2) Answer 2 📌📌📌 question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?For example, the polynomial identity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples AAPRD Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms;



2




Pdf The Group Of Primitive Almost Pythagorean Triples
Recognizing it as a difference of squares that can be factored as (x2 – y2)( x2 y2) Polynomial and rational ns at this level identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triplesIdentity (x2y2)2 = (x2– y2)2 (2xy)2 can be used to generate Pythagorean triples HSMP7 Look for and make use of structure HSMP8 Look for and express regularity in repeated reasoning AAPR4 Understand that polynomial identities include but are not difference of two squares, the sum and difference of two cubes, the square of a (Note sin (xy) = sin x cos y cos x sin y) F 2 sin 2x G 2 cos 2x H 2 sin 4x J 8 sin 2x K 8 cos 2x Can someone please explain how to do this problem to need help calculus plz plzsir steve if y=3e^(2x)cos(2x3) verify that d^2y/dx^24dy/dx8y=0 plz help me i tried all i could but it become too complicated for me here set u=3e^(2x) v=cos



Http M Hikari Com Ijma Ijma 14 Ijma 33 36 14 Catarinoijma33 36 14 Pdf




Type The Correct Answer In Each Box In Part E You Proved That Any Pythagorean Triple Can Be Brainly Com
For example, the polynomial identity (x² y²)² = (x² – y²)² (2xy)² can be used to generate Pythagorean triples Lesson/Activity Lesson/Activity Description Suggested TechnologyShow that it is true for quadratic polynomialsWrite a(x)/b(x) in the form q(x)




Formulas For Generating Pythagorean Triples Wikipedia




Pythagorean Triple From Wolfram Mathworld
For example, the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples D Rewrite rational expressions 6 Rewrite simple rational expressions in different forms;STANDARD AAPRC4 AII Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 –y 2) 2 (2xy) 2 can be used to generate Pythagorean triples WORKSHEETSThe answers to estudyassistantcom



2




Generating Pythagorean Triples 360
X 2 ( 1 2 y) x y 2 y − 2 Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factor The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;For example, the polynomial identity (x 22 y 2) = (x2 – y ) (2xy) can be used to generate Pythagorean triples Use complex numbers in polynomial identities and equations MGSE912NCN8 Extend polynomial identities to include factoring with complex numbers For example, rewrite x2 4 as (x 2i)(x – 2i) STANDARDS FOR MATHEMATICAL PRACTICE



Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions



Pythagorean Triples Generator Youtube
And x>y (x2−y2)2(2xy)2=(x2y2)2 If the sides of a right triangle are 57, 176, and 185, what are the values of x and y?Can be used to generate Pythagorean triples 4 Prove polynomial identities For example, prove the identity (x 2 y)= (x – y (2xy) or prove that the difference between squares of consecutive integers is odd Submit comments on the draft NYS Algebra II Mathematics Learning StandardsSelect two answers one for x and one for y 15 10



Math Questions Math Answers




Formulas For Generating Pythagorean Triples Wikipedia
X and y are positive integers;Polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples 318EX 318PR1 318PR5 14 5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle1Algebra 2 Arithmetic with Polynomials and Rational Expressions Guide The NMIS is a teacherinfluenced tool, designed to provide instructional planning support at the programmatic level for identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples
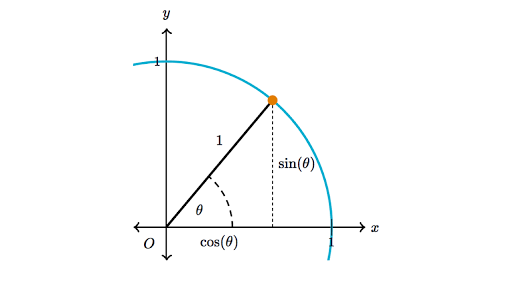



Pythagorean Identity Review Article Khan Academy




Pythagorean Triplet In An Array Geeksforgeeks
The polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples SE/TE CB 318 AAPR5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle SE/TE TE 330A330BAAPR4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples Rewrite rational expressionsLet t = x 2 y 2 xy then t xy ≥ 0 since it is the sum of two real squares x 2 y 2 and t xy ≥ 0 since it is the square of the real (x y) since (x y) 2 = x 2 y 2 2xy adding these, we get 2t ≥ 0, therefore t ≥ 0




Understanding Pythagorean Identities Studypug




Pdf Pythagorean Triples Before And After Pythagoras
Students will prove the polynomial identity ( x^2 y^2 )^2 ( 2xy )^2 = ( x^2 y^2 )^2 and use it to generate Pythagorean triples Use this activity as independent/partner practice or implement it as guided notes and practice for students in need of extra support Explan ation You have the quadratic equation 3x^2−10=−5 Then you must clear the variable "x" as below 3x^2−10=−5 3x^2=−510 3x^2=5 x^2=5/3 x= ±√ (5/3) When you multipy the numerator and the denominator by 3 for simplify the result, you obtainWrite a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree




Lesson 10 The Power Of Algebra Finding




A Apr 4 Objective Adding Amp Subtracting Polynomials Prove Polynomial Identities And Use Them



Pythagorean Triples
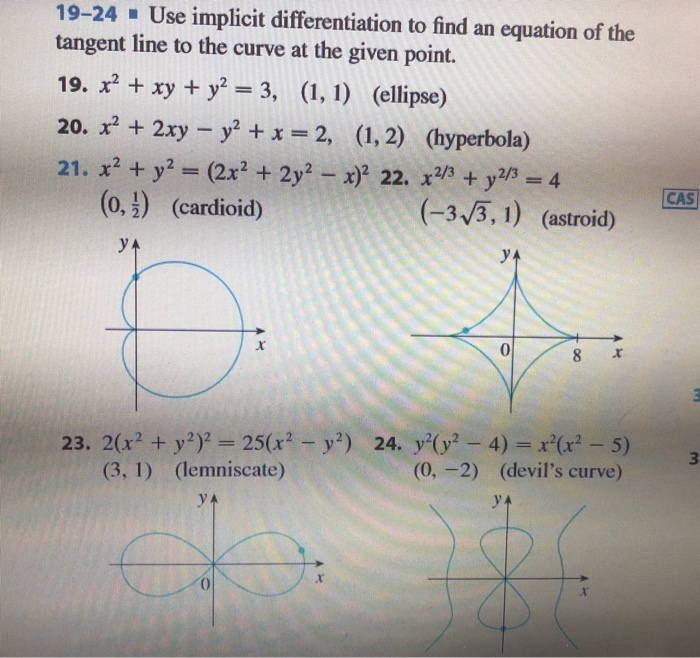



19 24 Use Implicit Differentiation To Find An Chegg Com



Generating Pythagorean Triples Chilimath




Generating Pythagorean Triples Chilimath



How To Find Pythagorean Triplets With One Given Number Quora




Curiousmathsknols Mathematics For The Curious Page 2




Pythagorean Triples Keith Conrad Pdf Free Download



1




Pdf Pythagorean Triples Before And After Pythagoras Ravi Agarwal Academia Edu



2




Eisenstein Triples Studocu




Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions




Mathgaz01 More Properties Of Pythagorean Triples Elementary Mathematics Number Theory



2



Http Www Veronaschools Org Cms Lib02 Nj Centricity Domain 18 Algebra 2 Pdf




Pythagorean Triples Keith Conrad Pdf Free Download



2



Pythagorean Triangles And Triples



2
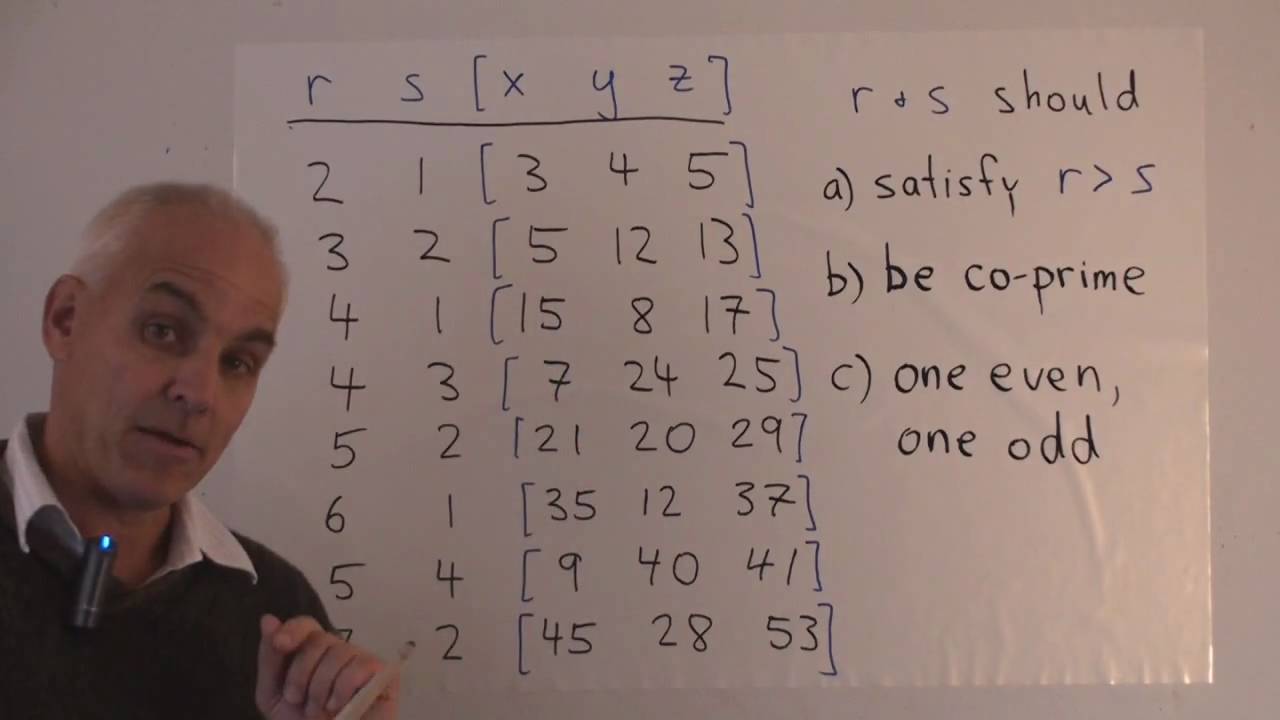



Pythagorean Triples Explanation Examples
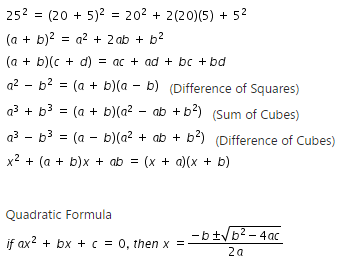



Mafs 912 A Apr 3 4 Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example The Polynomial Identity X Y X Y 2xy Can Be Used To Generate Pythagorean Triples




Calculus Set Free Infinitesimals To The Rescue Volume 1 Fall 19 Preliminary Edition By Bryan Dawson Issuu



Www Clarenceschools Org Cms Lib Ny Centricity Domain 465 Notes proving identities Pdf




Pythagorean Theorem An Overview Sciencedirect Topics



Pythagorean Triangles And Triples




Teaching Note Supply Tiles For Students A Apr 4 Objective Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example Ppt Download



2



Www Brewtoncityschools Org Cms Lib Al Centricity Domain 133 8 2 The Pythagorean Theorem And Its Converse Pdf



Www Fultonschools Org Cms Lib Ga Centricity Domain 1349 Algebra Ii Curriculum Map smf 19 Pdf



Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions




Honors Algebra 2 Amp College Algebra Central High School




Polynomial Identities And Pythagorean Triples Activity Polynomials Algebra Resources Algebra 2 Activities



Times Module M15 Pythagoras Theorem



Digitalcommons Gaacademy Org Cgi Viewcontent Cgi Article 1166 Context Gjs



2




8rdmath Flip Book Pages 1 50 Pubhtml5
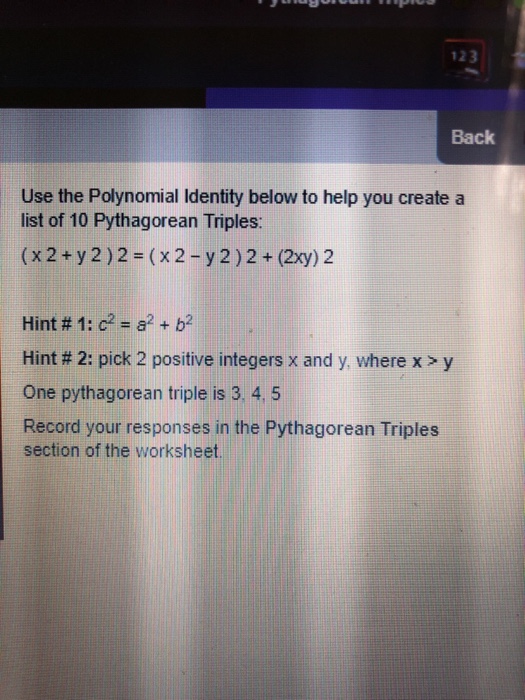



123 Back Use The Polynomial Identity Below To Help Chegg Com



1




Generate Pythagorean Triples Using An Identity Learnzillion



Q Tbn And9gctcnkr03soarrf1vsfmhkpwoqgnnut06hftvh9xjniw0r Zsimz Usqp Cau




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Algebra Ii Alignment Document




Understanding Pythagorean Identities Studypug




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download




How To Generate Pythagorean Triples Given The Sum Of The Triples Quora




Pdf The Modular Tree Of Pythagoras



Seeing Structure In Expressions Arithmetic With Polynomials And




Pythagorean Theorem How To Use Pythagoras Theorem With Examples



Http Www Admschools Org Wp Content Uploads 15 10 12 05 May 14 12 07 Pdf



How To Find Pythagorean Triplets With One Given Number Quora




Answered Example 3 Jeremy Uses The Polynomial Bartleby




Pythagorean Triples Keith Conrad Pdf Free Download




Pythagorean Triples Video Lessons Examples Step By Step Solutions



Pythagorean Triangles And Triples



Http Www Math Northwestern Edu Mlerma Problem Solving Putnam Training Problems 13 Pdf




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Q Tbn And9gcqps6qllmp1l0vsb5diwencc9bdlyhgrbtu3gebndt6gzbuls2f Usqp Cau




Pythagorean Triple From Wolfram Mathworld




Curiousmathsknols Mathematics For The Curious Page 2




Pythagorean Theorem Wikipedia



Pythagorean Triple From Wolfram Mathworld
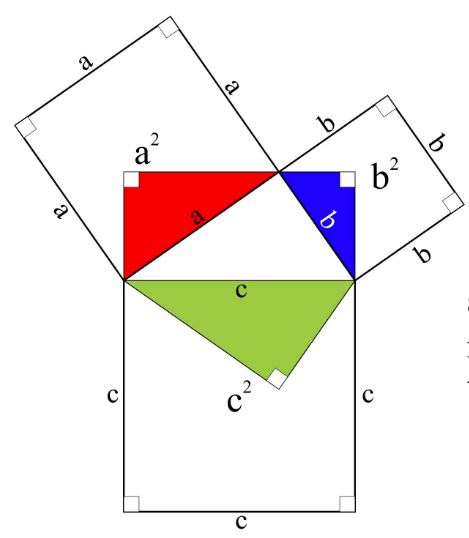



Pythagorean Theorem And Its Many Proofs



Http Pgsd Org Cms Lib07 Pa Centricity Domain 43 Hs algebra 2 Pdf




Use The Pythagorean Identity X2 Y 2 2xy 2 X2 Y2 2 To Create A Pythagorean Brainly Com




How To Use The Pythagorean Theorem With A Circle Veritas Prep




Polynomial Identities Solutions Examples Videos Worksheets Games Activities



2




Pythagoras Matrix Mathematics Determinant



2



Times Module M15 Pythagoras Theorem



2



2


