I'm Abhishek and today uploaded a new sum videoIStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2xy=6;2xy=2 Tiger Algebra Solver2x 1y = 6 3 Solve the following system x – y z = 0 x y read more
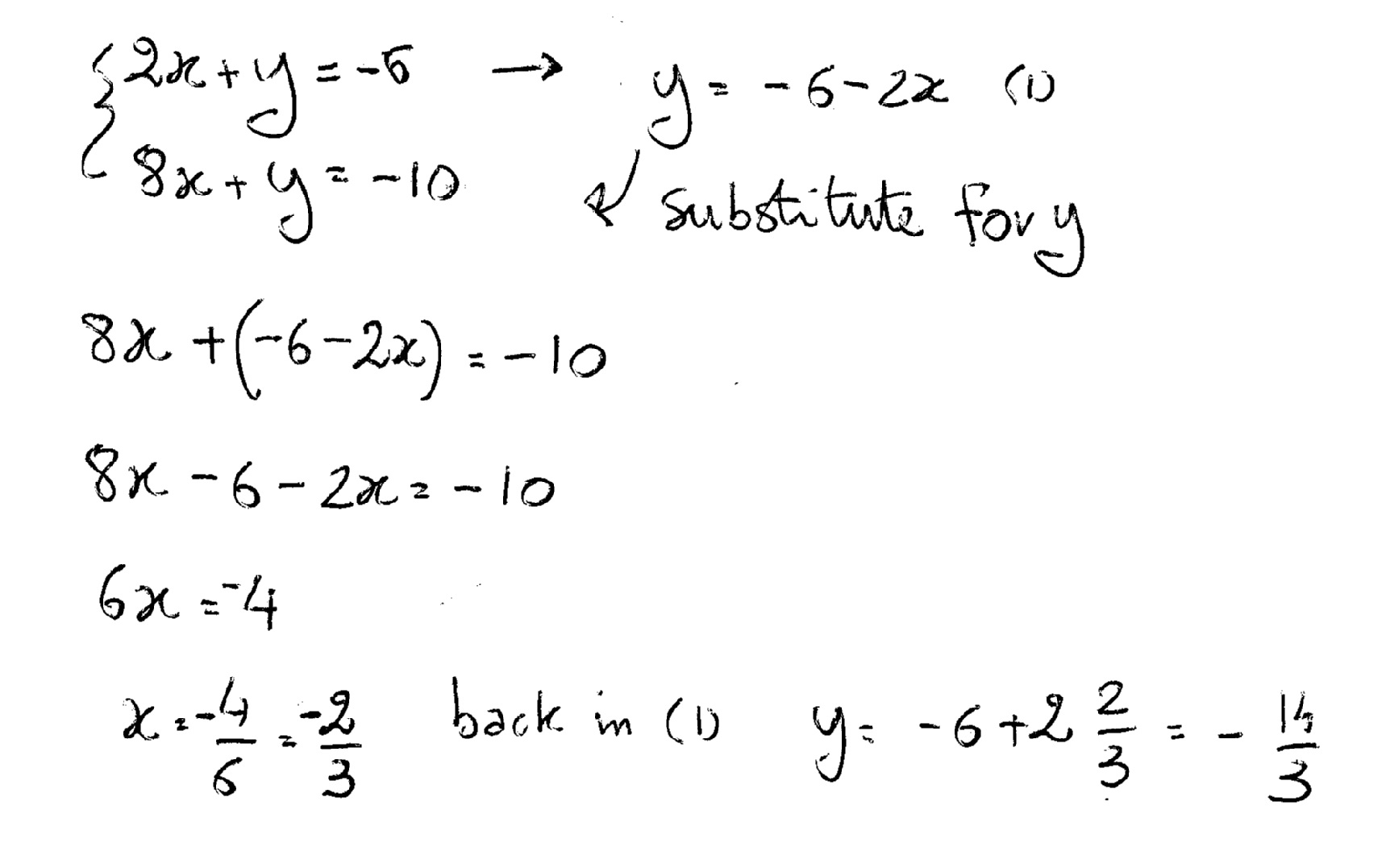
How Do You Solve By Substitution 2x Y 6 And 8x Y 10 Socratic
2x-y=6 x-y=2 by substitution method
2x-y=6 x-y=2 by substitution method- Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 − 6)/5 x = (25 − 6)/5 x = 𝟏𝟗/𝟓 Hence, x = 19/5,𝑦=6/5 Ex 34, 1 (Substitution Solve this system of equations using the Substitution Method y= 2x 10 and 2xy= 6 solve this system of equations using the Substitution Method y= 2x 10 and 2xy= 6 Categories English Leave a Reply Cancel reply Your email address will not be published Required fields are marked *




Solving Simultaneous Equations Equations And Inequalities Siyavula
The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematically2x y = 6 3x y = 6 Solve by Substitution // Solve equation 1 for the variable y 1 y = 2x 6 // Plug this in for variable y in equation 2 2 (2x 6) 3x = 6 2 x = 12 // Solve equation 2 forSolve by Substitution y=x6 , y=2x y = x 6 y = x 6 , y = 2x y = 2 x Eliminate the equal sides of each equation and combine x6 = 2x x 6 = 2 x Solve x6 = 2x x 6 = 2 x for x x Tap for more steps Move all terms containing x x to the left side of the equation
Solve the following pairs of linear equations by the substitution method 02x 03y = 13, 04x 05y = 23 asked in Mathematics by Samantha ( 3k Step 2 We use the substitution method to solve, from equation (1), y=2x6 (3) Now, substitute in equation (2) and solve for x, x 2 ( 2 x − 6) = 9 x 2 2 x − 6 = 9 x 2 2 x − 15 = 0 x 2 5 x − 3 x − 15 = 0 Substitution Method Use the Substitution method to solve the system of equations x y = 4 x y = 2 x y = 4 x y = 2 In the second equation, x= y2 Putting that in the first (y2) y= 4 subtract two from each side, then divide each side by
Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!* *Response times may vary by subject and question complexity Median response time is 34 minutes for paid subscribers and may be longer for promotional offersSubstitution Method Use the Substitution method to solve the system of equations x y = 4 x y = 2 x y = 4 x y = 2 In the second equation, x= y2 Putting that in the first (y2) y= 4 subtract two from each side, then divide each side by algebra Solve the following system using the substitution method 3x y = 3 y = 2x 7Solve The Following Pair Of Linear Equation By Substitution Method 2x Y 2 And X 3y 15 Brainly In For more information and source, see on this link https//brainly




Solve X Y 2x Y 6 2x Y 2 By Elimination Method Maths Pair Of Linear Equations In Two Variables Meritnation Com




Solve X And Y X 6 Y 4 1 And 3x 4 X Y 2 7 4 Related Substitution Method Pair Of Linear Equations In Two Variables Edurev Class 10 Question
Solve the following pair of linear equations by the substitution method (3x)/2 (5y)/3 = 2, x/yy/2 = 13/6 CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3111 Question Bank Solutions 334 Concept Notes &Answer to Solve using the substitution method 4x 2y = 6; Algebra Please use the substitution method to solve the linear equation y=3x and y=2x6 Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora



Solve The Following Systems Of Equations X Y 2xy X Y Xy 6 X 0 Y 0 Sarthaks Econnect Largest Online Education Community
To use the substitution method, first isolate one of the variables in one of the equations Isolate the "y" in the first equation (because it is the easiest to isolate), and substitute it into the second equation 2x y = Subtract 2x on both sides y = 2x 5y = 6x 12 (since y = 2x, you can substitute 2x into y) Example 32 1 Solve by substitution { 2 x y = − 3 3 x − 2 y = − 8 Solution Solve for either variable in either equation If you choose the first equation, you can isolate y in one step Substitute the expression − 2 x − 3 for the variable y in the other equation Figure 32 1Solve by Substitution Calculator Step 1 Enter the system of equations you want to solve for by substitution The solve by substitution calculator allows to find the solution to a system of two or three equations in both a point form and an equation form of the answer Step 2 Click the blue arrow to submit



Solve The Following Systems Of Equations X Y Xy 2 X Y Xy 6 Sarthaks Econnect Largest Online Education Community




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy
Substitution Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm144Steps for Using the Substitution Method in order to Solve Systems of Equations Solve 1 equation for 1 variable (Put in y = or x = form) Substitute this expression into the other equation and solve for the missing variable Substitute your answer into the first equation and solve Check the solutionSolve the system of equations by using the addition method Write the answer in simplest form 1) a) 06x – 04y = 01 b) 2x 08y = 02 The solution set is Solve the system by using any method If a system does not have on unique solution, state whether the system is inconsistent or whether the equations are dependent 1) a)3x




Solve The System X Y Z 6 X Y Z 2 2x Y Z 1 Using Matrix Inverse Youtube



Who Can Solve This X Y 15 And X Y 3 Find X And Y Quora
Substitution Method In the substitution method the simpler equation is transposed to make one of the variables the subject, and then substitution enables the second equation to be reduced to one variable Examples 1 Solve the simultaneous equations x y = 6 1 and x – y = 2 2 It is convenient to label the equationsPlease watch "Abhishek Medly 6 Zack Knight " https//wwwyoutubecom/watch?v=osa3Alk2SBM ~Hi Guys!Solve the following pairs of linear equations by the substitution method 02x 03y = 13, 04x 05y = 23 asked in Mathematics by Samantha ( 3k




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3
We are given two equations, one of which has y as its subject Substitute the expression 2x 6 for y in the second equation y = 2x 6 and 2x − y = 2 × × × × × 2x − (2x 6) = 2 × × × × × 2x − 2x −6 = 2 × × × × × × × ×x0 = 8 This is obviously false and there is no x left This is an indication that there is no possible solution to this equationAnswer to Solve the system by the method of substitution a) y = 2x^2 y = x^4 2x^3 b) x^2 y^2 = 169 3x 2y = 39 By signing up, for Teachers for Schools for Working Scholars® for CollegeThe following steps will be useful to solve system of linear equations using method of substitution Step 1 In the given two equations, solve one of the equations either for x or y




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




Solve X Y 14 X Y 2
The substitution property says that a quantity may be replaced with its equal In a linear system of equations, substitution results in one equation with one variable The solution to a linear system is an ordered pair, not just a single value There may be no solution or an infinite number of solutionsCorrect answer to the question Substitution method 2xy=6 2xy2=0 brainsanswersincomFree system of equations calculator solve system of equations stepbystep




Solve The Following Pair Of Linear Equation By Substitution Method 3x 2y 7 0 4x Y 6 0



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic
If the following three equations hold simultaneously for xand y, find p 3x−2y=6,3x −6y =21 ,x−py=6 EASY View Answer Solve the following pair of equations by substitution methodSubstituting x in (2) we get, 2(16−3y)−y = 4 ⇒ 32−6y−y = 4 −6y−y = 4−32 −7y = −28 y = −7−28 = 4 Substituting y =4 in (3) we get, x = 16−3(4) = 16−12 = 42x 3 = y By signing up, you'll get thousands of stepbystep solutions to your




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15




Solve The Following System Of Equations By Method Of Cross Mult
Solve The System By The Method Of Substitution Check Your Solution(s) Graphically ſ 2x Y = 6 {xy=0 (X,Y) 2 9 O/1 Points DETAILS PREVIOUS ANSWERS LARAT10 Solve The System Graphically (If There Is No Solution, Enter NO SOLUTION) {x 2y =Get an answer for 'Y=6x11 3x2y=7 solve by substitution' and find homework help for other Math questions at eNotesSo for our problem we 1) Solve the second equation for y I chose the second equation and y because y has no coefficient by it in the second equation (well except 1 but that doesn't matter) 2xy=6 Subtract 2x from both sides to get y by its self y = 2x6* Divide both sides by 1 to get y by its self y = 2x6




X Y 6 X Y 4 Practice Set 1 2 Simultaneous Equation Graphically Graph Method Grade 10 Youtube




Solve By Substitution Method X Y 11 2x 3y 7 Brainly In
This will give us an equation with just one variable, 'x' Adding y to both sides gives us 2x=y2 Then subtracting 2 from both sides gives us y=2x2 Subtracting 2x from both sides gives us y=2x6 Since we have both equations set equal to 'y', we can plug one equation into the other Secondary School answer answered TOL Solve by substitution method x y = 2 and 3x – 2y = 16 1 See answer plus Add answer 5 pts report flag outlined 1 Solve by using the substitution method x 6y = 28 6x 6y = 18 2 Solve by using the elimination method x 2y = 12 &nbs p;




Example 4 Check Whether Equations X 3y 6 And 2x 3y
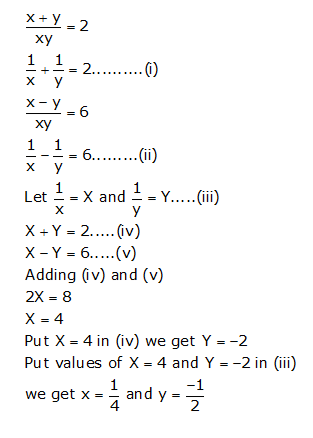



Solve The Following System Of Linear Equations X Y 2 X Y 6 Xy Xy Mathematics Topperlearning Com D9jn35dd
Solve by substitution method x 2y = 1 and 2x 3y = 12 Get the answer to this question and access a vast question bank that is tailored for students Using substitution in this case means plugging in x 2 for y (for example), since they are stated to be equal y = 2x − 2X&Xy = x 2 Therefore, 2x − 2 = x 2 XXXXXXXX2x = x 4 XXXXXXXXXx = 4 Now we know that x = 4, so plug in x to one of the equations in order to find y y = x 2 y = 4 2Use the substitution method to solve the following system of linear equations x y = 6 x = –y 2




X Y 14 X Y 4 Solve Using Substitution Method Youtube



Solved Find The Common Solution Of Each Using The Elimination And Substitution Method 2x Y 2 X 3y 36 B Course Hero
Substitution Method Steps Step 1 Solve one of the equations for one of its variables Step 2 Substitute the expression from step 1 into the other equation and solve for the other variable Step 3 Substitute the value from step 2 into either original equation and solve to find the value of the variable in step 1Substitution method can be applied in four steps Step 1 Solve one of the equations for either x = or y = Step 2 Substitute the solution from step 1 into the other equation Step 3 Solve this new equation Step 4 Solve for the second variableSolution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0




2x 3y 10 And X Y 4 By Substitution Method Brainly In



Solve For X And Y Using Substitution Method 2x 5y Xy 6 And 4x 5y Xy 3 Where X And Y Are Not Brainly In
(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3Check in both equations by substituting (x,y)= (2,2) and see if it equals out L1) (2)2 (2)=6 24=6 6=6 L1 checks out L2) (2)=2 (2)6 2=46 2=2 L2 checks out also, so we can say with confidence that the solution indeed is (x,y)= (2,2) Happy Calculating!!!2xy6=0, 4x2y4=0 solve by substitution, elimination And graph Maths Pair of Linear Equations in Two Variables



How To Solve For X And Y In X Y 5 And Xy 6 Quora




2x Y 6 X Y 2 By Cross Multiplication Method Brainly In



Solve The Following Systems Of Equations Xy X Y 6 5 Xy Y X 6 Sarthaks Econnect Largest Online Education Community




Thumb M Mathpresso Io Qanda Thumbnail Storage Q




X Y 6 X Y 2 Find Out Value Of X And Y Brainly In



The Substitution Method




6 X Y 7 X Y 3 1 2 X Y 1 3 X Y



Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 603 A1 c6 l2 solution key worked out Pdf




Solve The Pair Of Equation X Y Xy 2 X Y Xy 6 Brainly In




Solve By Substitution Method X Y 2 3x 2y 16 Brainly In




Solutions F X 6x 2 6xy 24x F Y 3x 2 6y To Find The Critical Points We Solve Pdf Free Download




Draw The Graph Of The Equations 2x Y 6 0 And 2x Y 6 0 Also Determine The Coordinates Of The Vertices Of The Triangle Formed By These Lines And The X Axis
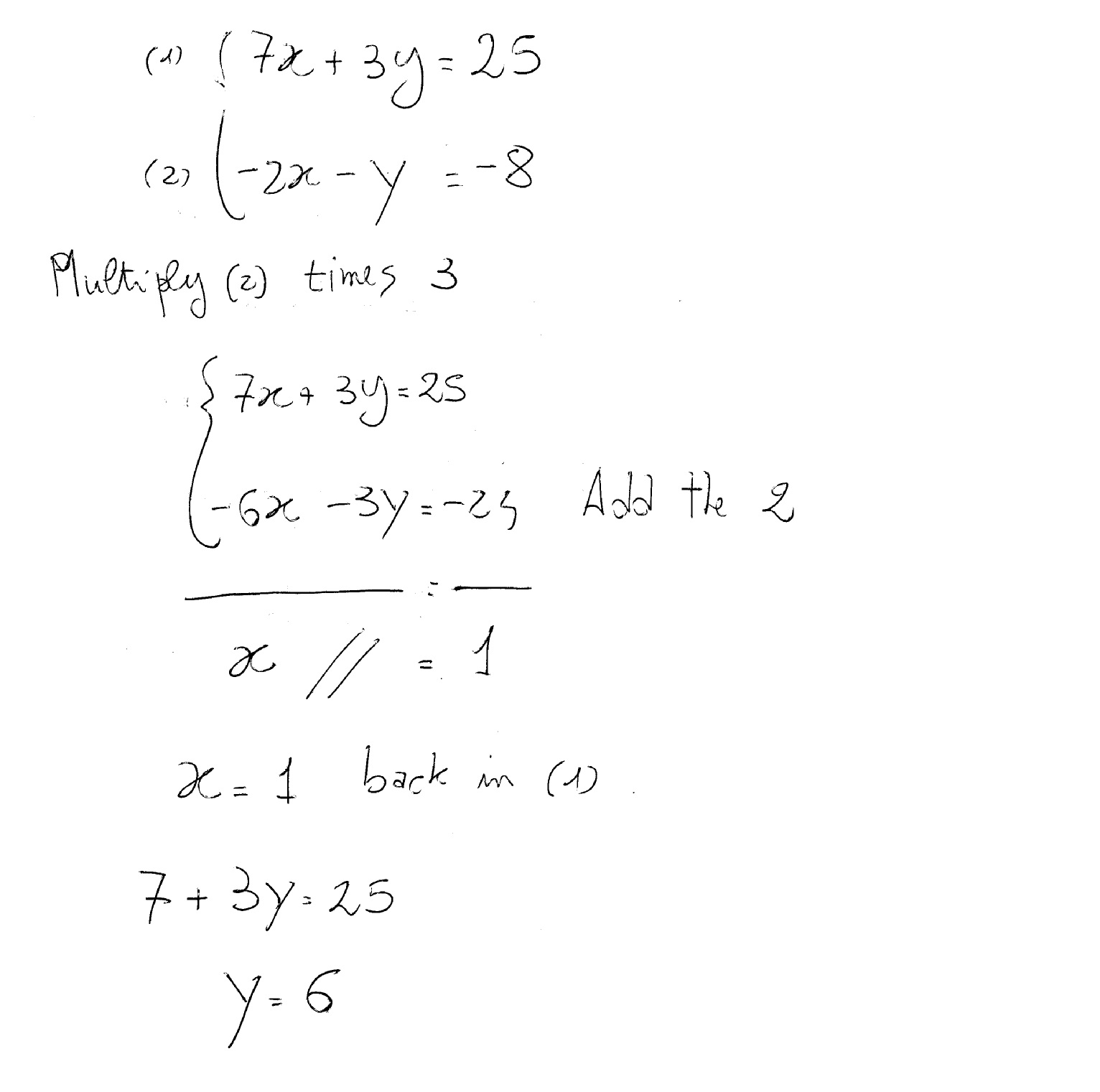



How Do You Solve The System 7x 3y 25 And 2x Y 8 Socratic



What Are X And Y From The System Equation 2x 3y 4 X Y 6 Quora




X3y10 X Y 2 2x Y 6 Xy3 X2y18 See How To Solve It At Qanda




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr



Solve Each Of The Following Systems Of Equations By The Method Of Cross Multiplication 2x Y 6 0 X Y 2 0 Sarthaks Econnect Largest Online Education Community




Solve The Given Differential Equation By Using An Chegg Com
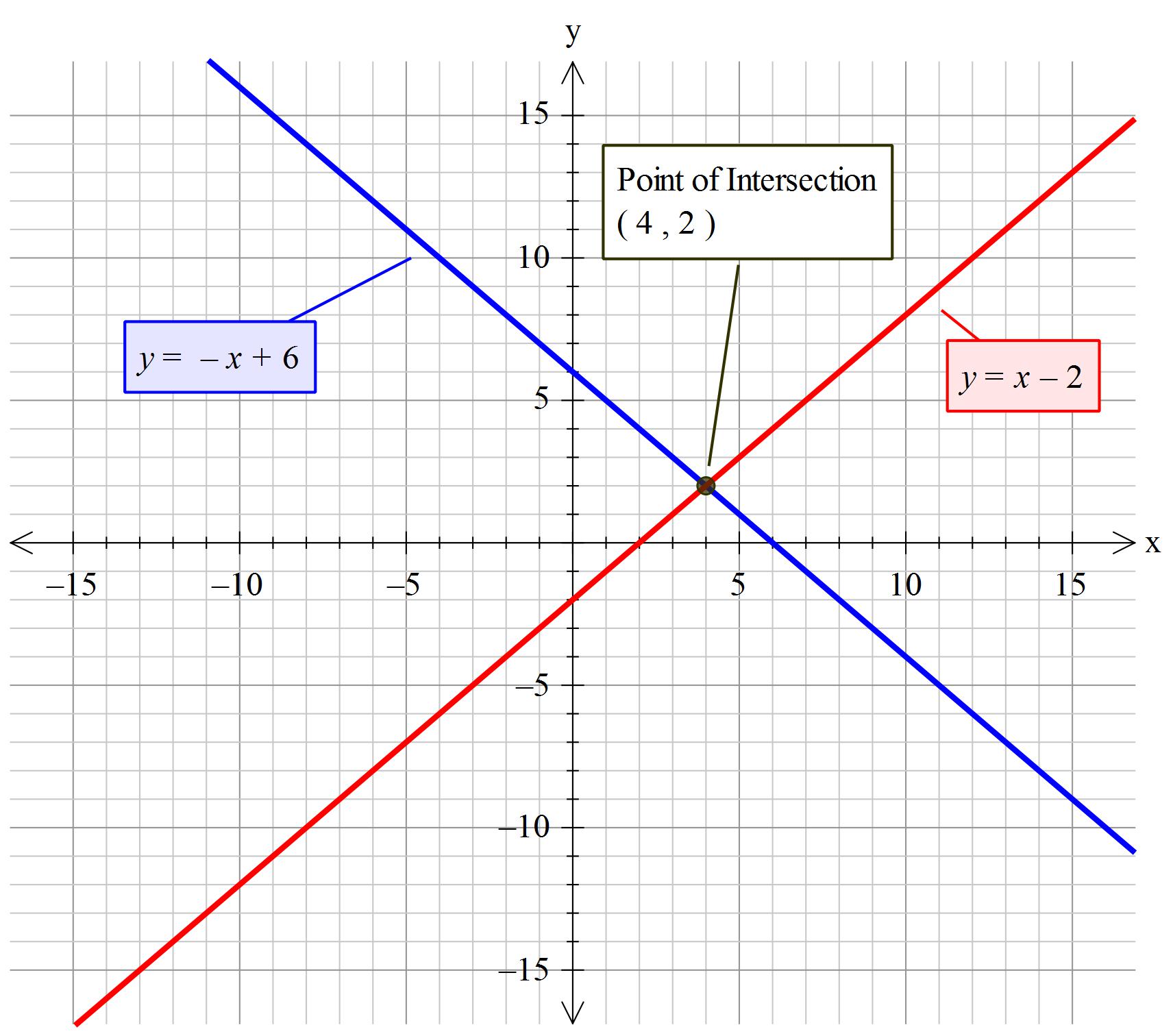



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic




X Y Xy 2 And X Y Xy 6 By Elimination Method Brainly In




Solutions F X 6x 2 6xy 24x F Y 3x 2 6y To Find The Critical Points We Solve Pdf Free Download




Do Now Solve Each System Using Elimination 2x 3y 8 X Y 2 Ppt Video Online Download




Find The Asymptotes Of The Following Curves Y 3 3x 2y X Y 2 3x 3 2y 2 2x Y 4x 5y 6 0 Youtube
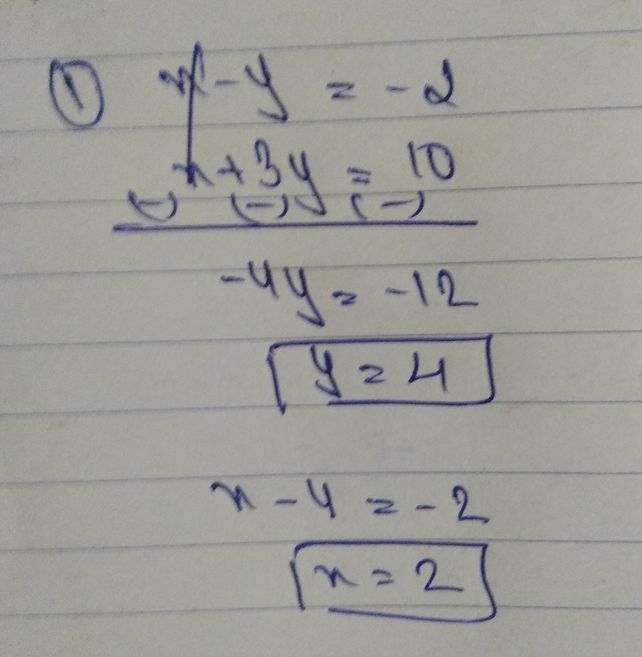



X3y10 X Y 2 2x Y 6 Xy3 X2y18 See How To Solve It At Qanda




Solve The Following System Of Equations By Substitution Method 1 X Y 14x Y 2 Brainly In



The Substitution Method




1 Solve The Following Pair Of Linear Equations By The Substitution Method 1 X Y 14 Ii S T 3 S 6 X Y 4 Ii 3x Y 3 9x 3y 9 3 2 Iv 0 2x 0 3y 1 3 0 4x




Consider The Differential Equation Xy 2 Bx 2y Dx Chegg Com




Solve 2x Y 6 And 2x Y 2 0 By Elimination Method Brainly In




3 Systems Of Linear Equations




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com




2x Y 6 X Y 2 By Elimination Method Brainly In
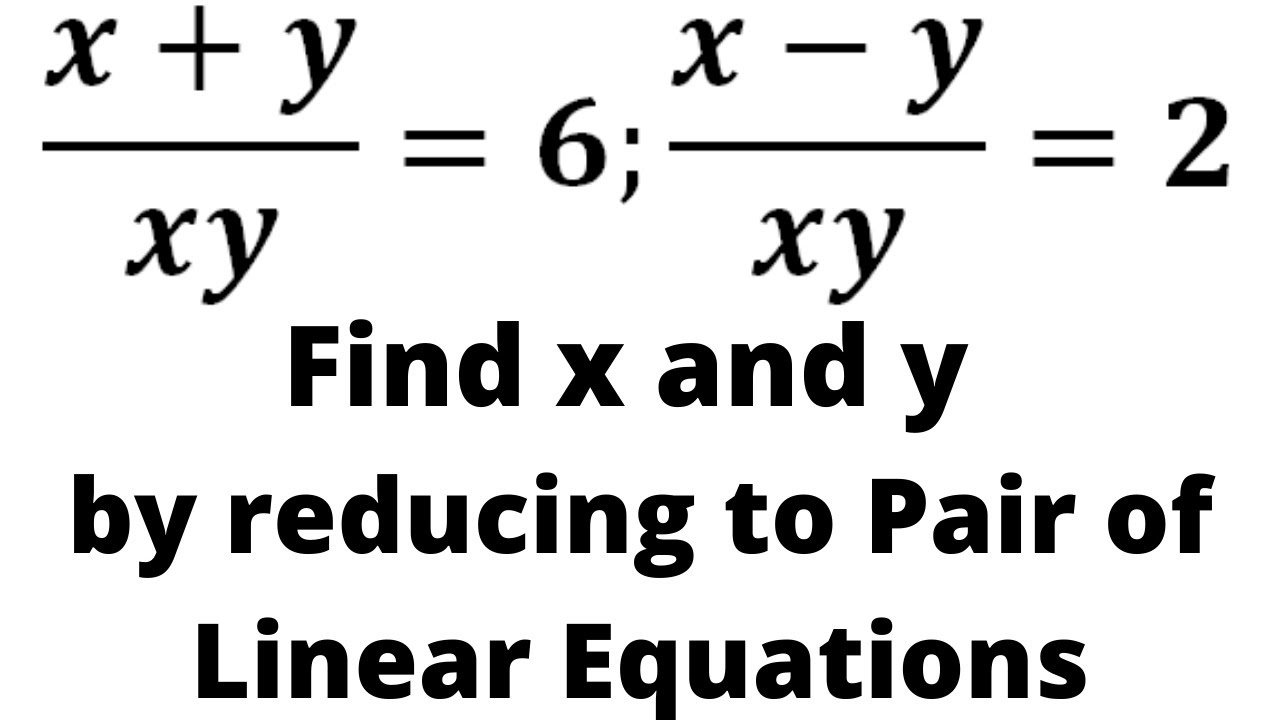



X Y Xy 6 X Y Xy 2 Find X And Y By Reducing Them To Pair Of Linear Equations Youtube




Solve The Following System Of Equations 5 X Y 2 X Y 1




X Y 2xy X Y 6xy Solve By Substitution Method Maths Pair Of Linear Equations In Two Variables Meritnation Com




Solve For X And Y 2x Y 6 And X Y 2 Brainly In




Solve The Equation 2x Y 6 0 And 2x Y 2 0 By Substitution Method Brainly In
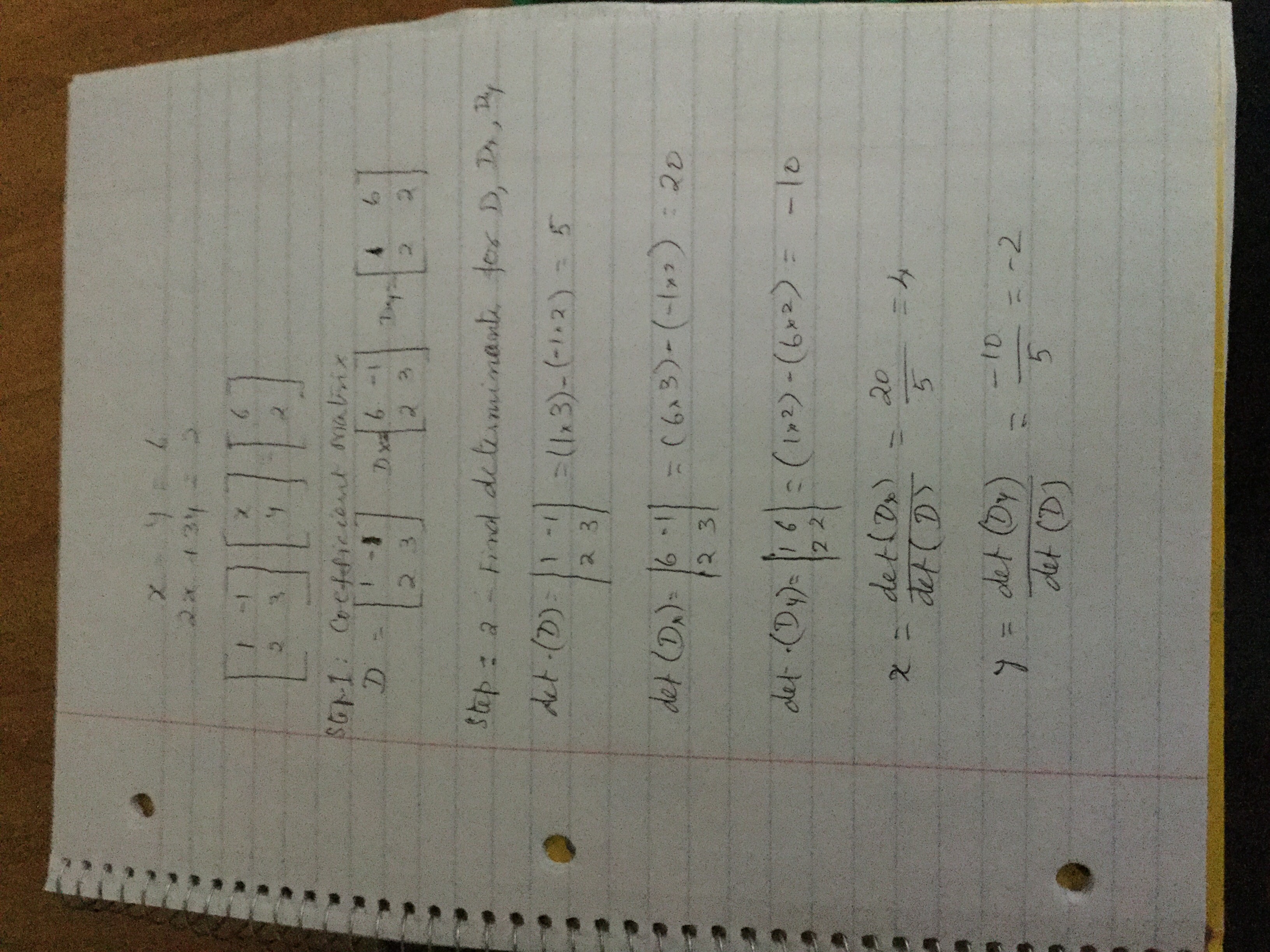



How Do You Solve X Y 6 And 2x 3y 2 Using Matrices Socratic



Simultaneous Equations Gmat Math Study Guide



What Is X And Y When X Y 10 And X Y 6 Simultaneous Equation Quora



What Is The Answer To Find The Equation Of The Line Through The Point Of Intersection Of Lines X Y 6 0 And 2x Y 3 0 And Passing Through The Point 2 1 Quora




2x X Y 6 2 X 2x Y 3 1 Mathematics Topperlearning Com Fqktm544



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero



Solved Find The Common Solution Of Each Using The Elimination And Substitution Method 2x Y 2 X 3y 36 B Course Hero




Solve The Pair Of Linear Equations By Substitution Method X Y 6 X Y 2 Brainly In
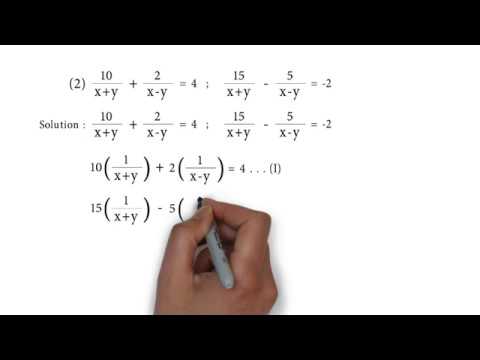



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt



Solve Each Of The Following Systems Of Equations By The Method Of Cross Multiplication 2x Y 6 0 X Y 2 0 Sarthaks Econnect Largest Online Education Community



Solve The Following Systems Of Equations X Y Xy 2 X Y Xy 6 Sarthaks Econnect Largest Online Education Community




Solve The Following System Of Equations By Method Of Cross Mult



1




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




J19
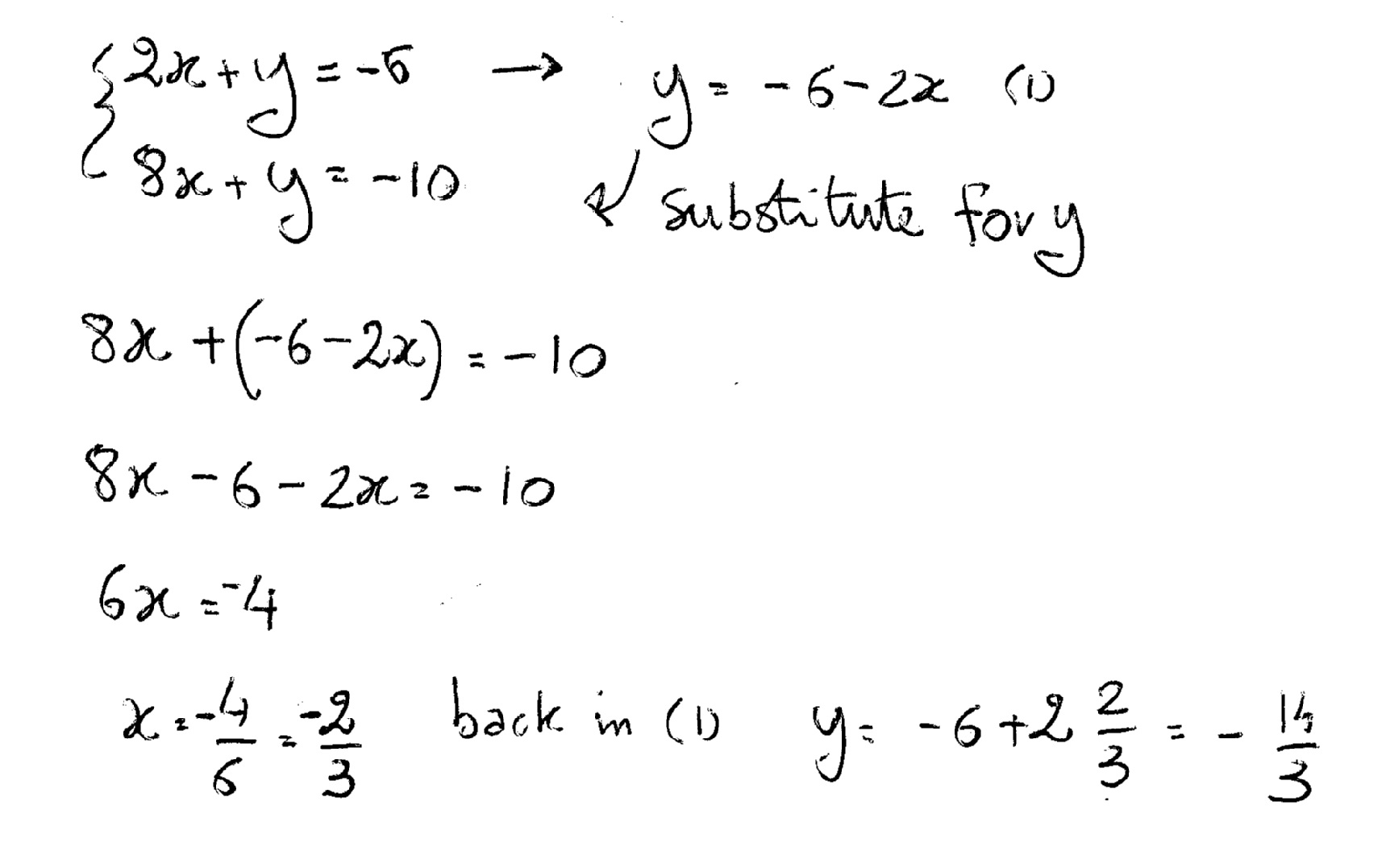



How Do You Solve By Substitution 2x Y 6 And 8x Y 10 Socratic
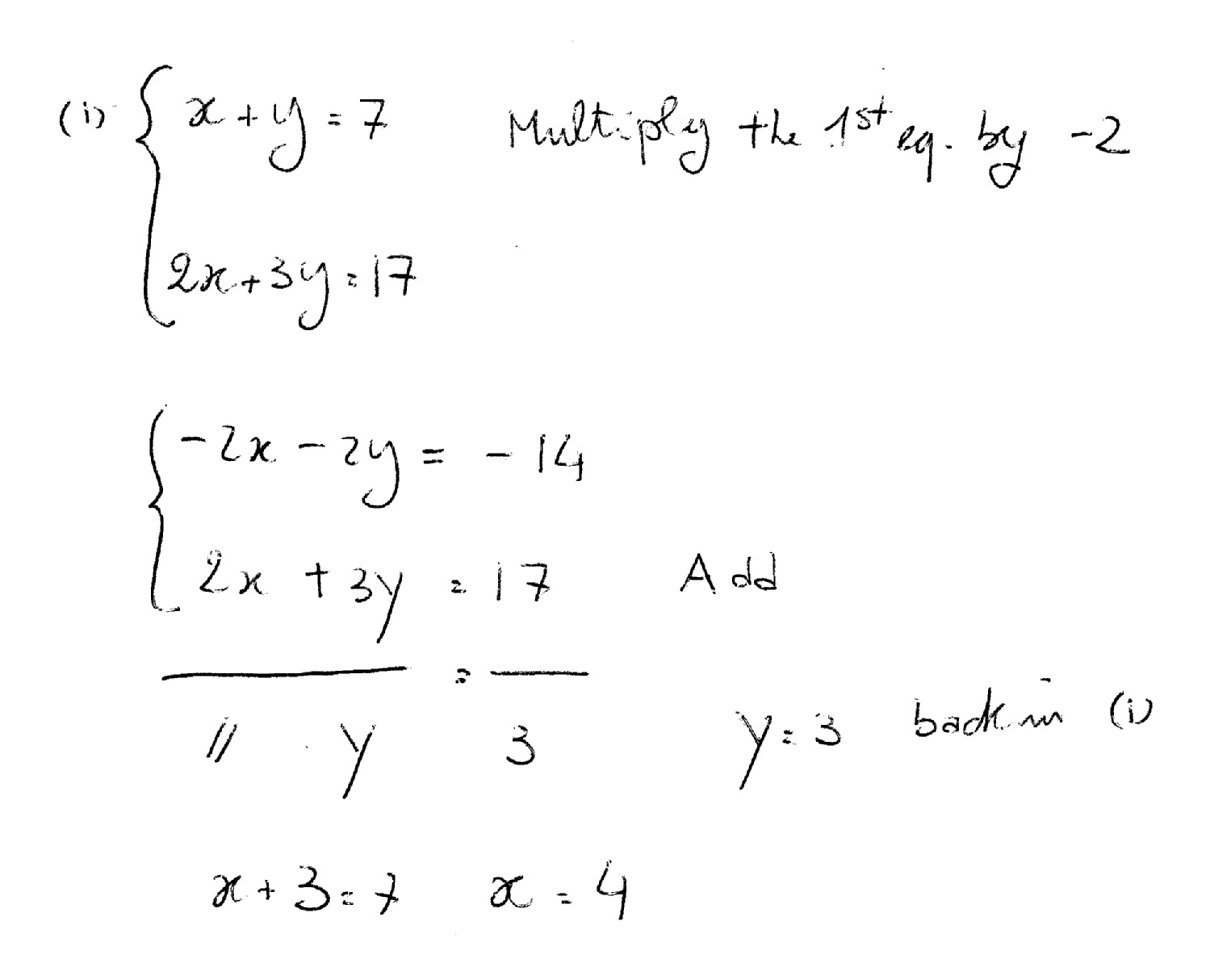



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic
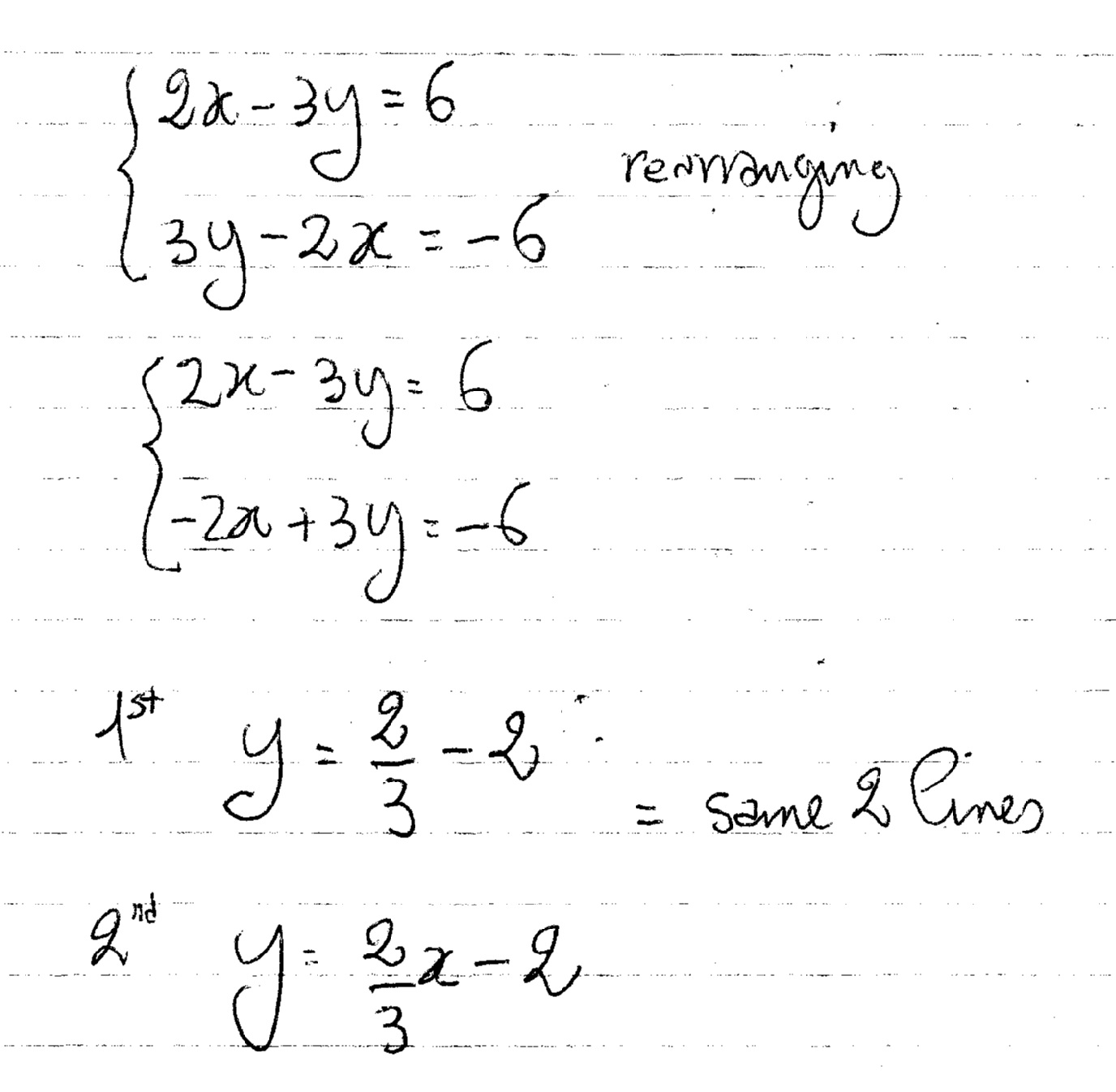



How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic




2x Y 11 And X Y 8 Solve Using Substitution And Elimination Method Youtube




Solving Simultaneous Equations Equations And Inequalities Siyavula
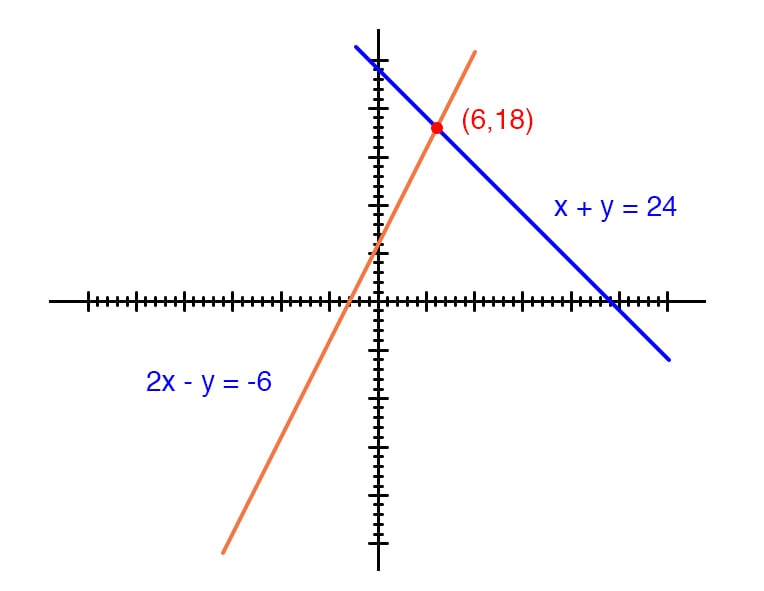



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook




Solve The Following System Of Equations By Method Of Cross Mult



Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 603 A1 c6 l2 solution key worked out Pdf




Systems Of Equations Elimination Part Ii Unit 7 Lesson 5b Ppt Download




How To Solve This Differential Equation Math 1 X 2 Y 6xy 4y 0 R T Math Quora




Each De In Problems 1 14 Is Homogeneous In Problems Chegg Com



How To Solve For X And Y In X Y 5 And Xy 6 Quora




1 Solve The Following Using Graphical Method 12 Chegg Com




Solve The Following Pair Of Linear Equation By Substitution Method I X Y 2 3x 2y 16 Brainly In




Solved Solve The System Of Equations Using The Substituti Chegg Com
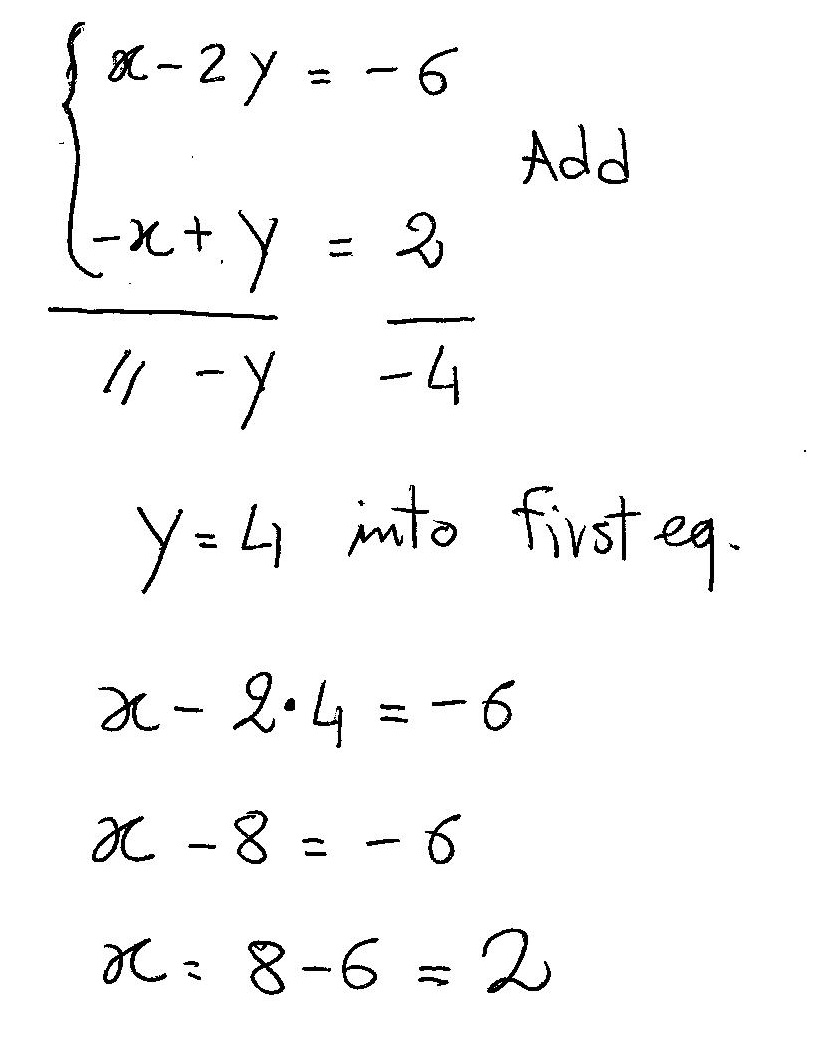



How Do You Solve X 2y 6 And X Y 2 Socratic




Consider The Following Cauchy Euler Equation X 3 Y Chegg Com
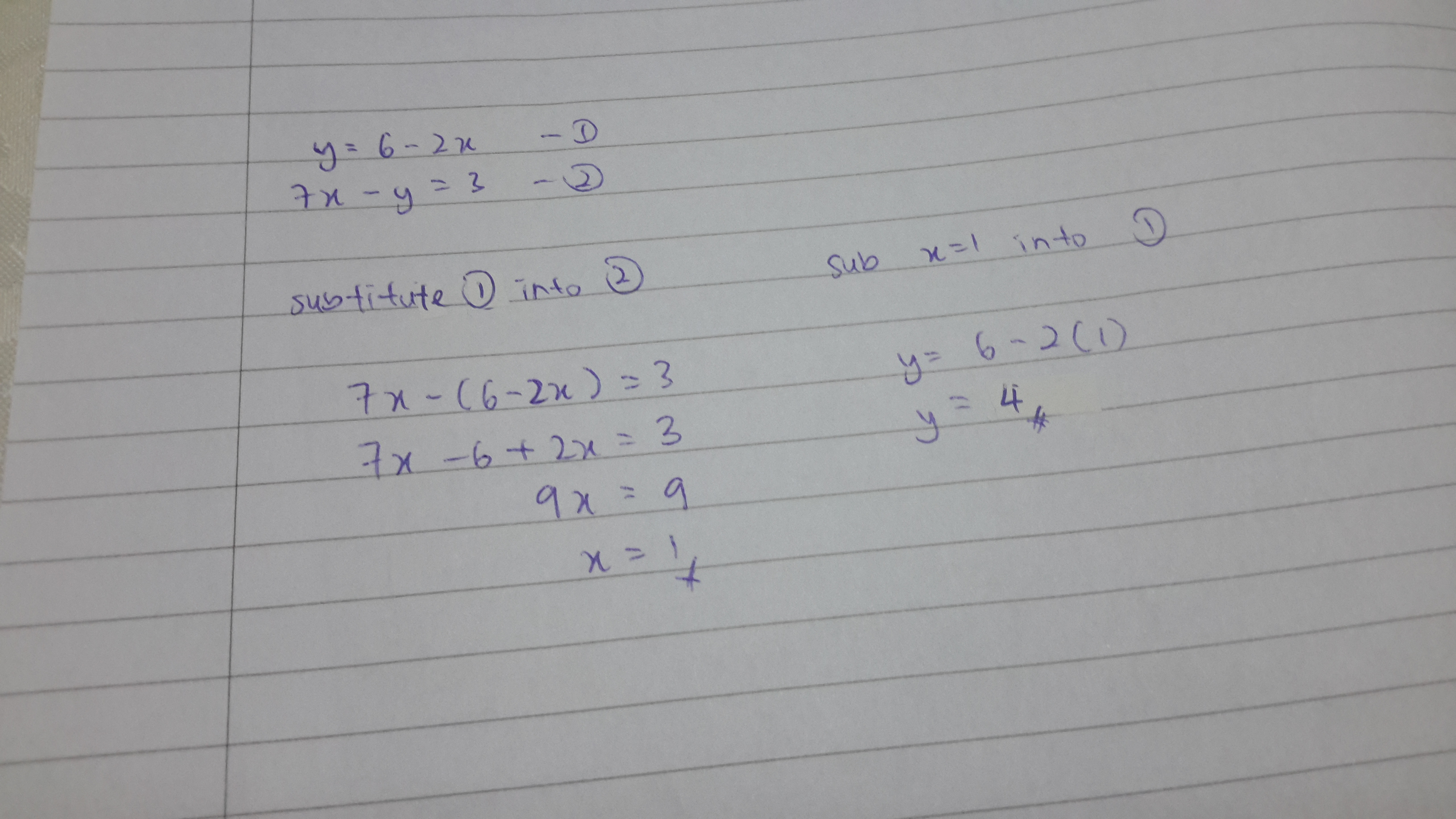



How Do You Solve The Following Linear System Y 6 2x 7x Y 3 Socratic



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community



Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic



The Elimination Method


